What is Clustering?

Clustering is one of the most popular unsupervised classification techniques used in machine learning. We can divide the data into clusters using clustering methods based on centroids, distributions, and densities. There are various clustering methods, with K-means and hierarchical clustering being among the most popular.

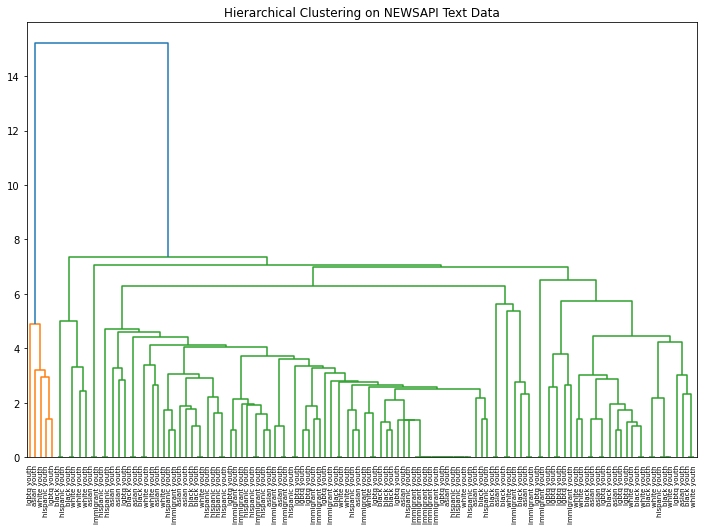
Clustering Record Data in R

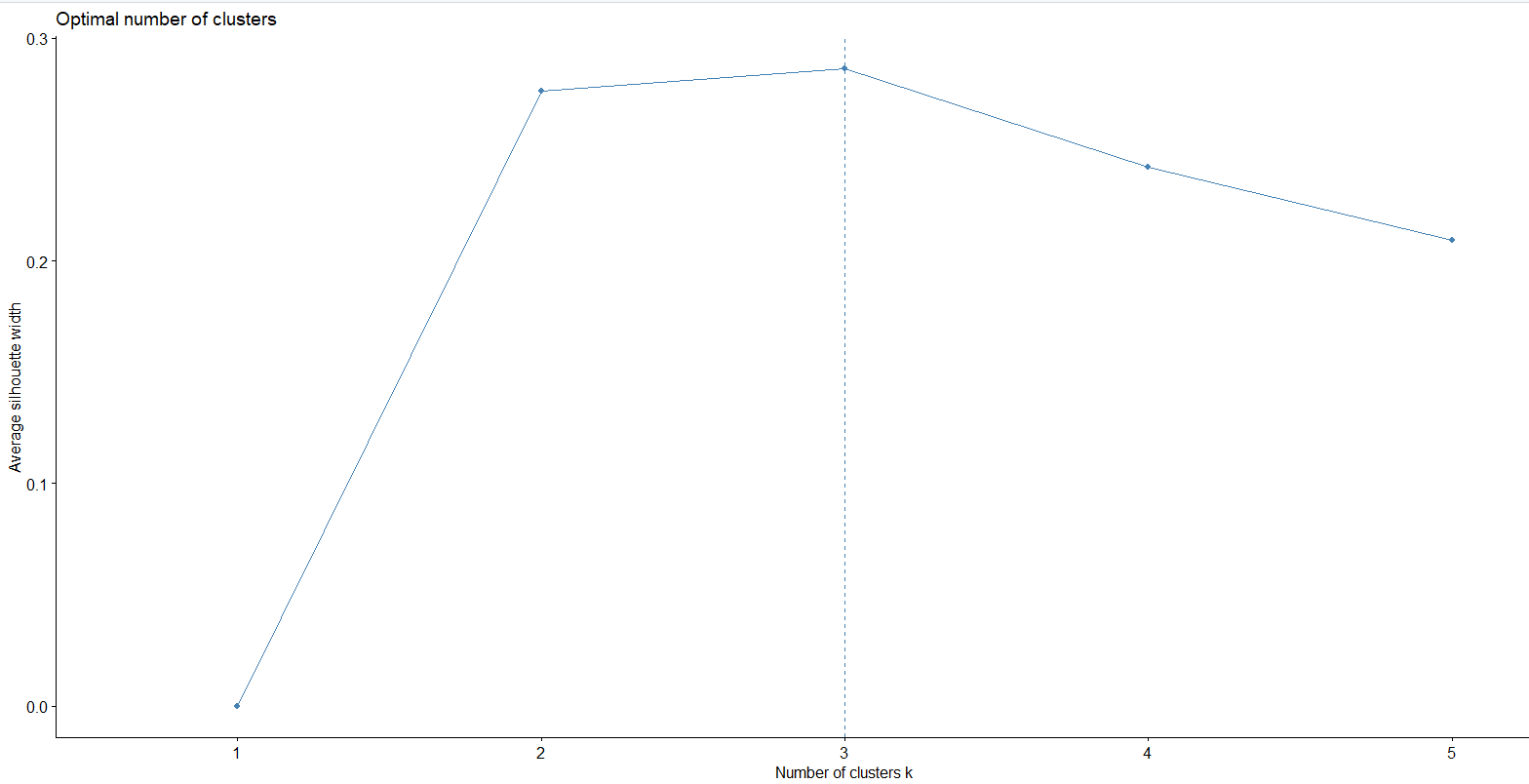
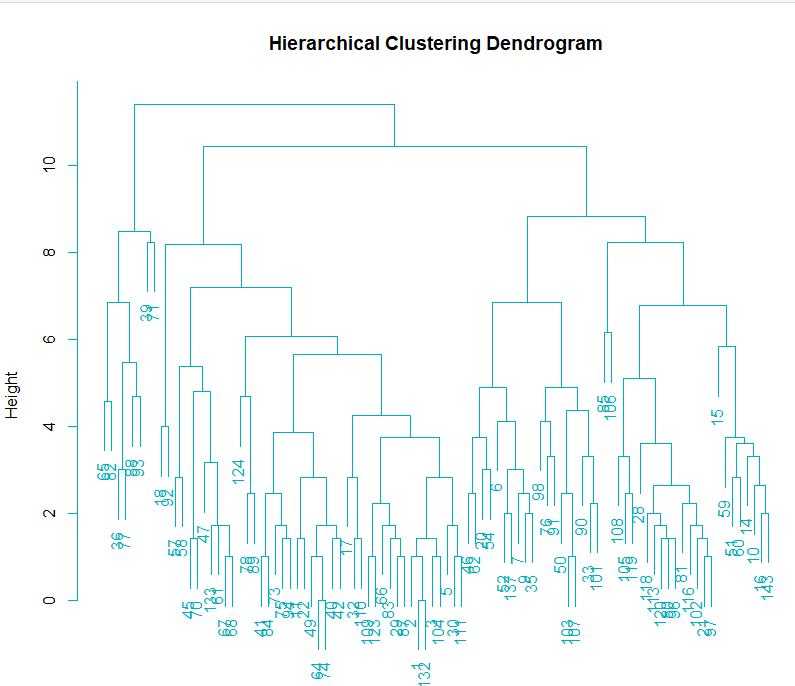
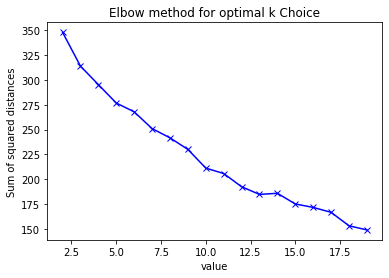
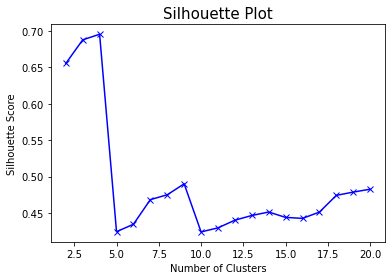
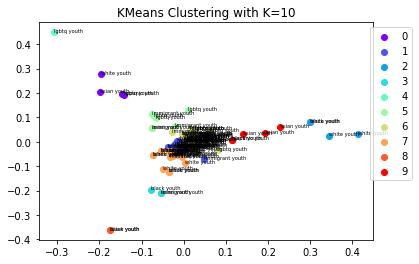
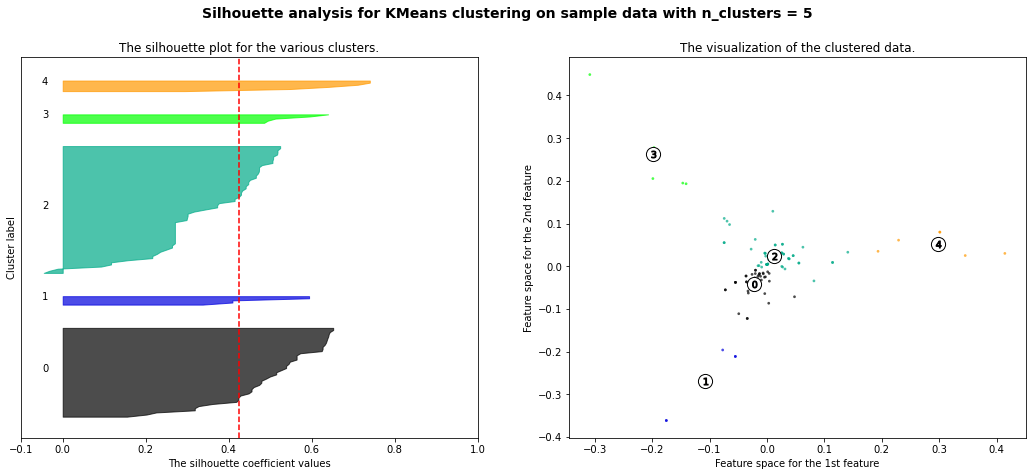
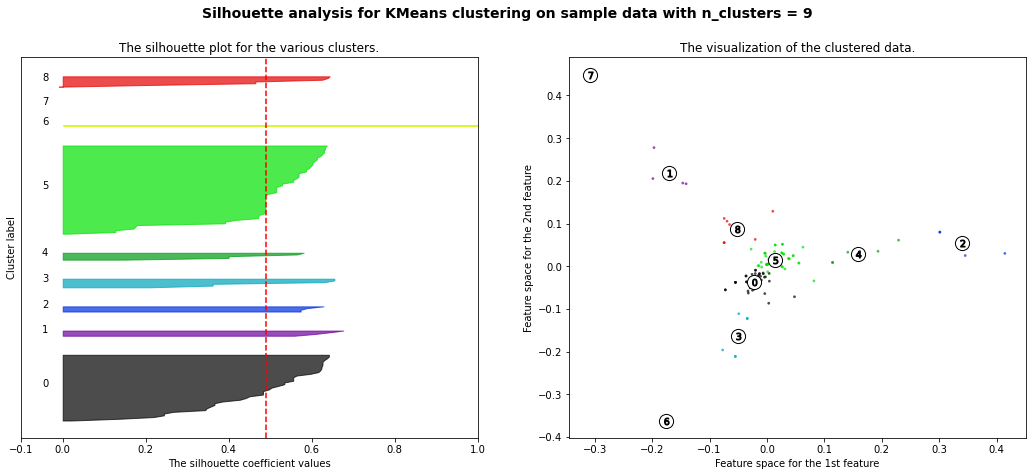
Clustering analysis was performed using the YRBSS dataset. The data contains categorical variables including gender, race, sexual orientation, whether one carries a weapon, whether one gets in physical fights, feelings of sadness, whether one has considered attempting suicide, whether one has made plans to attempt suicide, and more. All the labels were removed from the data to conduct clustering.Link to dataset & code: Clusterings dataset. R code used.

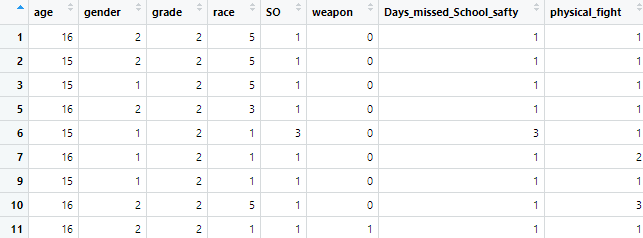
Figure 1a: Dataset Prior to Cleaning

Source: Youth Risk Behavior Surveillance System (YRBSS) Survery Data

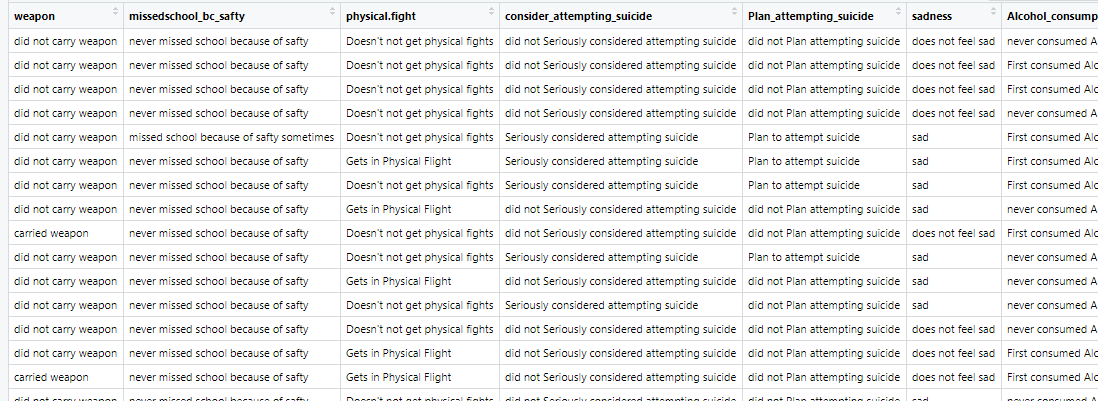
Figure 1b: Clean Dataset

Source: Youth Risk Behavior Surveillance System (YRBSS) Survery Data

Determining the Best Number of Clusters in the Data Usings Slihouette and Elbow

Figure 2a:Elbow Curve

Elbow curve was calculated using the Euclidean measure of distance.The visual above, we can see the largest change between k=3 and k=4, implying that the best number of clusters is 3.

Figure 2b: Silhouette Curve

Silhouette score is a metric used to calculate the goodness of a clustering technique. The visual above, we can see the largest score in the datasets occures k=3, also implying that the best number of clusters is 3.

K-means Clustering

K-means clustering is a nonhierarchical clustering method. It is an iterative method that aims to allocate n observations into k clusters, where each observation belongs to the group with the nearest mean. K-means considers every point in a dataset and uses the information to evolve the clustering over many iterations. In k-means clustering, the value for k, the number of clusters, does need to be specified. It is crucial to choose an appropriate value for k. If k is too small, a category may be missed or combined with another. If k is too large, there is a risk of overfitting the data. The worst case of this overfitting occurs when k equals the number of vectors, n. In Figure 3a, above, you can see that four clusters were created using k values of 1, 2, 3, and 4. It is worth noting that the vast majority of the data is concentrated close to each other, resulting in overlapping each cluster. According to the Elbow Curve in Figure 2a and the Silhouette Curve in Figure 2b, the best optimal number of k equals 3.

In Figure 3a, above, you can see that four clusters were created using k values of 1, 2, 3, and 4. It is worth noting that the vast majority of the data is concentrated close to each other, resulting in overlapping each cluster. According to the Elbow Curve in Figure 2a and the Silhouette Curve in Figure 2b, the best optimal number of k equals 3.

Figure 3a: K-Means Clustering

Note: K-means clustering using YRBSS dataset.

Hierarchical clustering

Hierarchical clustering separates data into different groups based on some measure of similarity. Just like the name, it involves some form of hierarchical and this can be done by either joining or dividing. The joining method begins by linking the individual observations closest to each other in space defined by the dimensions used in the analysis. Joined with other clusters or individual observations to create larger clusters. This process continues until all observations are joined together into a single cluster.

Euclidean distance is the distance between two points in coordinate geometry. In machine learning, euclidean distance calculates the distance between two real-valued vectors in the dataset to measure the similarity. The dendrograms in Figure 4 was created after changing the dataset into a euclidean distance matrices

Figure 4: Hierarchical Clustering of YRBSS dataset

Figure 3b: Euclidean Heatmap

Clustering in Python

Clustering analysis was performed using the News API dataset.Link to dataset & code: Clusterings dataset. Python code used.

Figure 4a:Elbow Curve

Figure 4b: Silhouette Curve

Figure 4c: Scatter plot after preforming PCA

Using three different methods - Silhouette, Elbow, and DBSCAN, the figures above illustrate the best way to estimate the values of k. According to the elbow curve in figure 4a, the best estimate of k is at k=8. However, the plot also shows a noticeable dip at k=14. In figure 4b, we can see the average silhouette scores had the most significant value at k = 5, indicating that the best number of clusters is 5. According to the elbow curve, the best estimate of k is at k=8. However, the plot also shows a noticeable dip in the plot at k=6 and k=13. The DBSCAN, shown in figure 4c, there are 10 distinct clusters.

K-means Clustering

Figure 5a: K-Means Clustering

Figure 5b: K-Means Clustering

The different k-means clustering values all seemed to produce interesting results.

Hierarchical clustering

Figure 6: Hierarchical Clustering of News API dataset

The dendrogram in figure 6 was created using cosine similarity metrics. The results from the dendrogram above don't show interesting results.

Quote of the day:"If you torture data long enough, it will tell you whatever you want to hear."