ARIMAX
The ARIMAX (Autoregressive Integrated Moving Average with Explanatory Variables) model is an extension of the ARIMA model that allows for the inclusion of additional explanatory variables to help explain the behavior of the dependent variable in a time series analysis. In the ARIMAX model, the dependent variable is still modeled as a function of its past values and the past errors of the model, but now it is also modeled as a function of one or more exogenous (i.e., independent) variables that are believed to influence the behavior of the dependent variable. These exogenous variables can be any type of variable, such as economic indicators, demographic factors, or weather data. The ARIMAX model is often used when there are other variables that may have a causal relationship with the dependent variable, and the inclusion of these variables can help improve the accuracy of the time series model. The model can be estimated using maximum likelihood estimation or other statistical methods, and the accuracy of the model can be evaluated using various metrics such as mean squared error or root mean squared error.
Literature Review
A study by Choi (2022) compared the housing price forecasting performance in Korea, the USA, and Japan using the ARIMA, GARCH, and RS models. The analysis was performed on the in-sample and out-of-sample forecasting performance of the models with the forecasting period. In Korea and the USA, the forecasting performance of the ARIMA model was higher than that of the GARCH or RS models, while the EGARCH model performed better than the ARIMA model or RS model in Japan. Regarding the out-of-sample forecast, the short-term forecasting performance was higher than the long-term forecasting performance, which is consistent with general theory. The RS model that can grasp a structural change possibility, including stagnant and boom markets, can be a helpful alternative for forecasting performance improvement, as the housing price forecasting term is longer. The study suggests that there is a need to identify a model, data, and research periods suitable for each market for housing price forecasting power improvement. Similarly, Malmendier and Alexandra (2023), recently published a paper that examines the impact of inflation experiences on homeownership across 21 countries over a period of four decades. The findings from their paper suggests that countries with higher inflation rates experience lower rates of homeownership, and the effect is particularly pronounced for younger cohorts. The paper also shows that inflation shocks can have long-term effects on homeownership rates, as the negative impact persists even after inflation rates return to lower levels. The study further demonstrates that macroeconomic stability, financial development, and legal protection of property rights are important factors that influence the relationship between inflation experiences and homeownership rates.
Figure 1.
Data Selection
Above, we see the relationship between the homeownership rate and the other variables in the dataset, including the interest rate, the unemployment rate, median home income, personal savings rate, and median home sold.
Fitting the Data Using auto.arima
Figure 2.
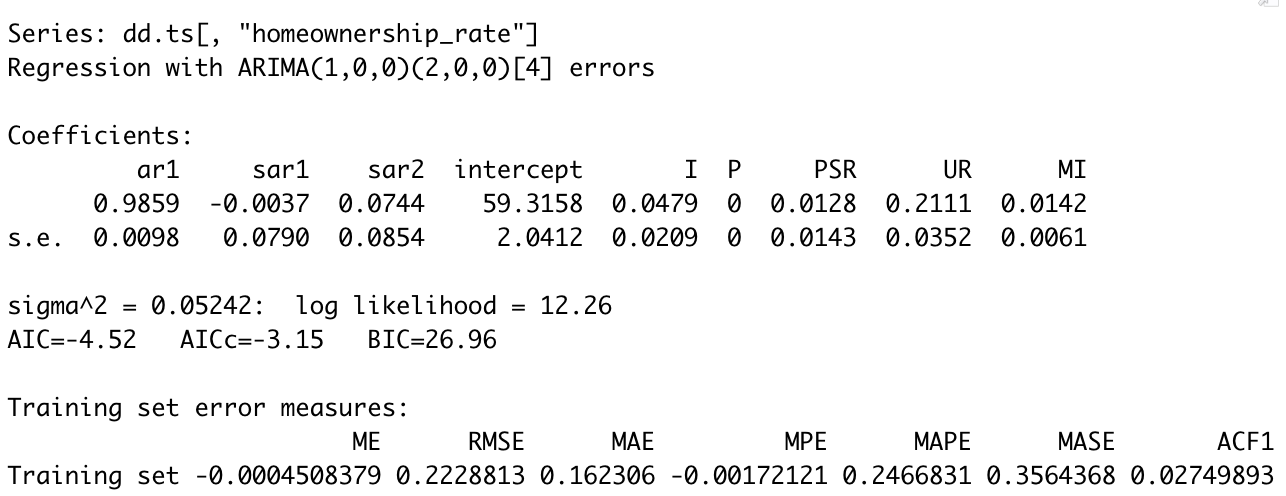
Figure 3. Auto.Arima output

The auto Arima selected ARIMA(1,0,0)(2,0,0)[4] to be the best model.
Fitting the model manually
Figure 5.
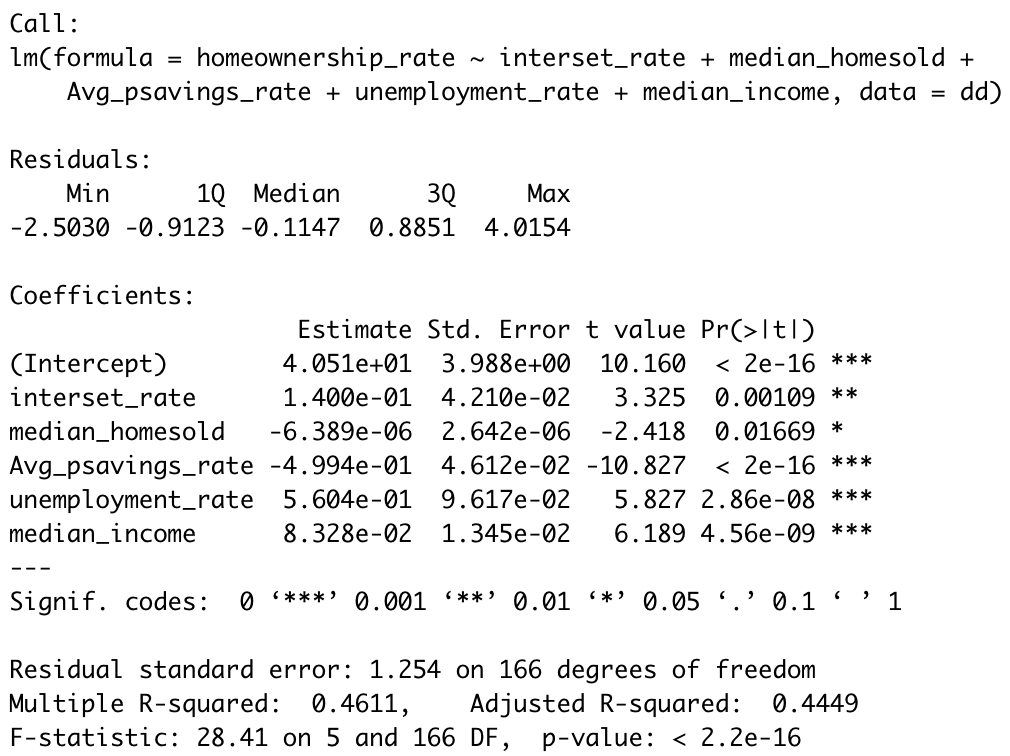
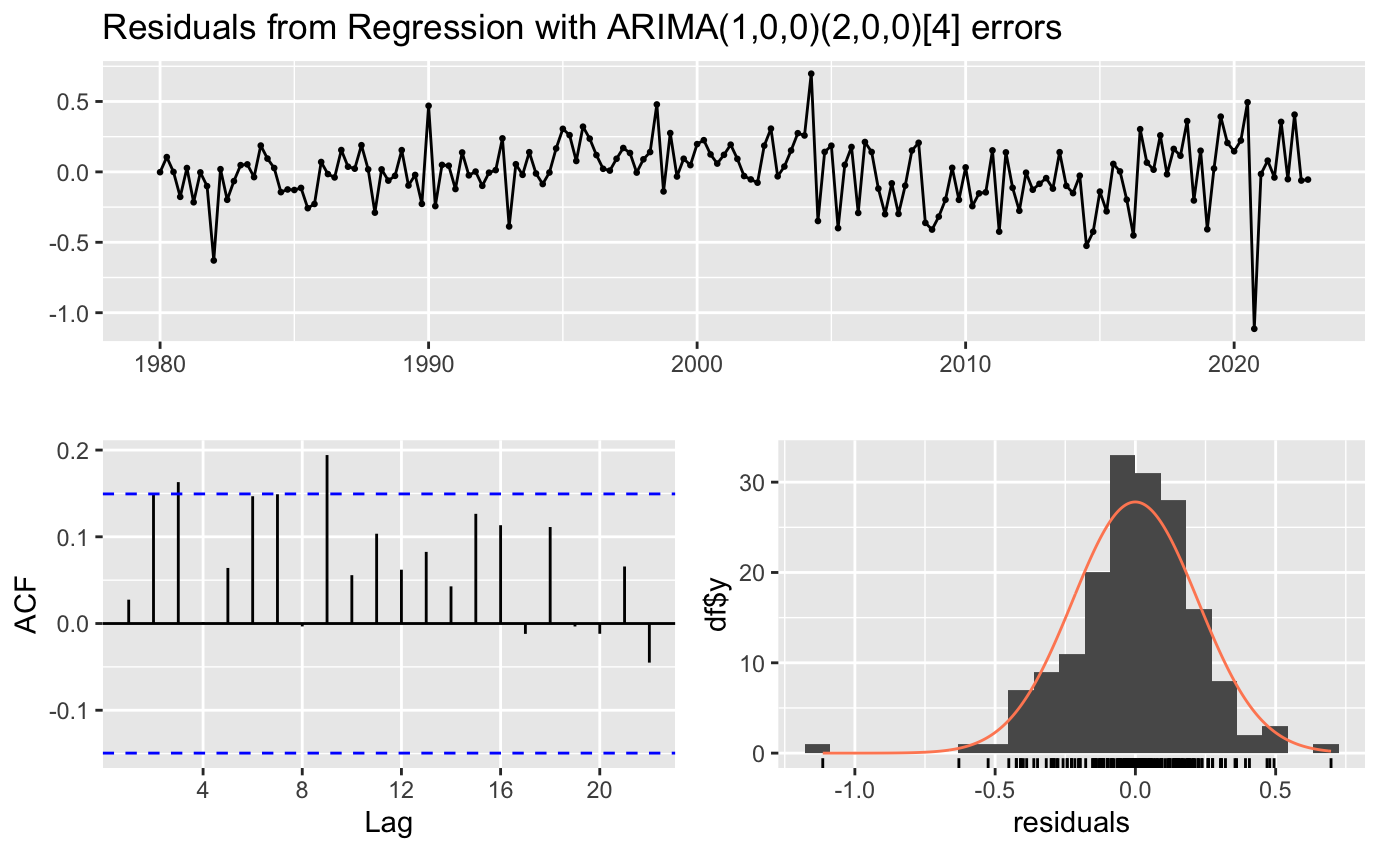
Figure 6. Manual Fit ACF Plot
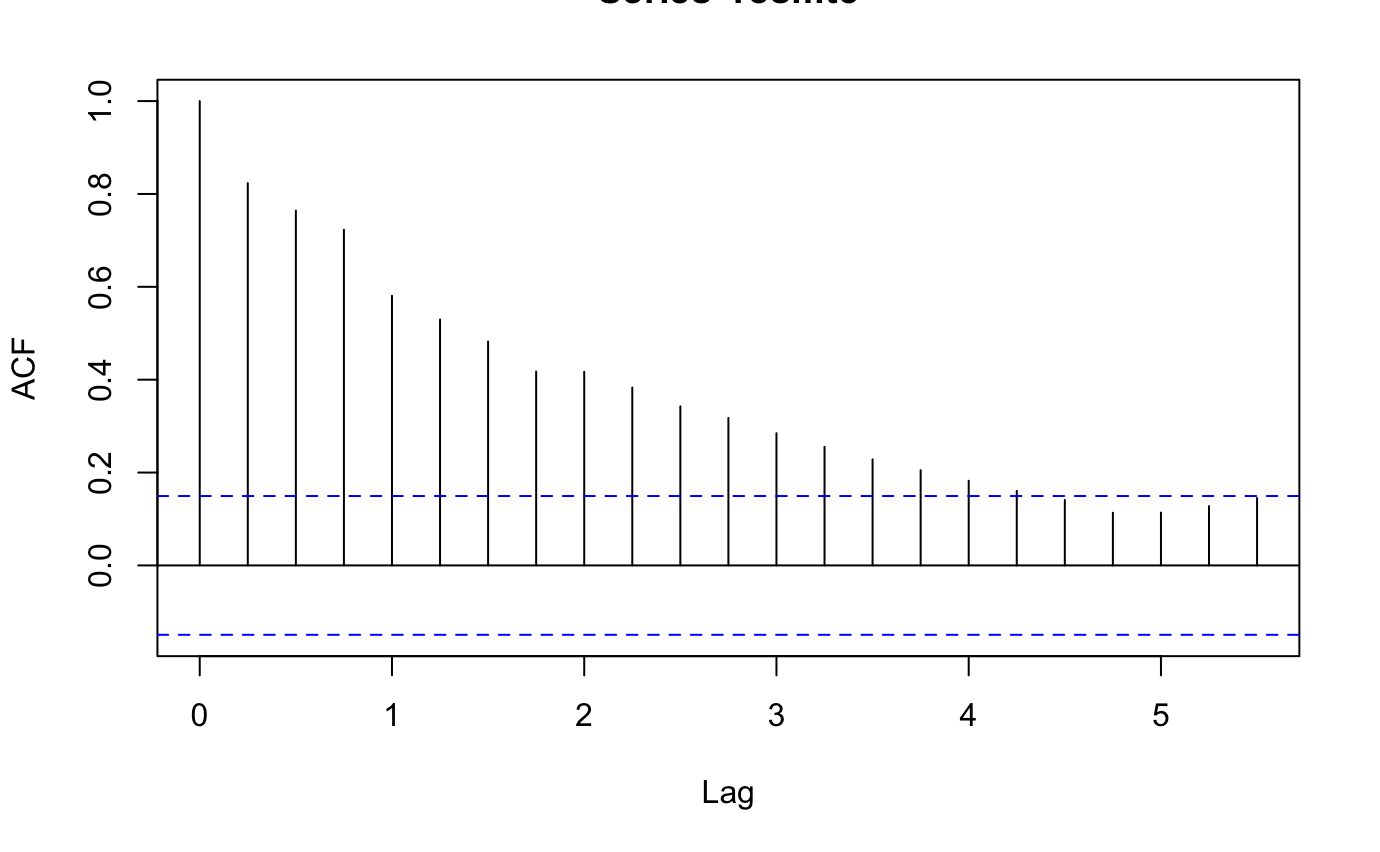
The lags in ACF are significant so difference is needed.
Figure 7.Differencing Plots
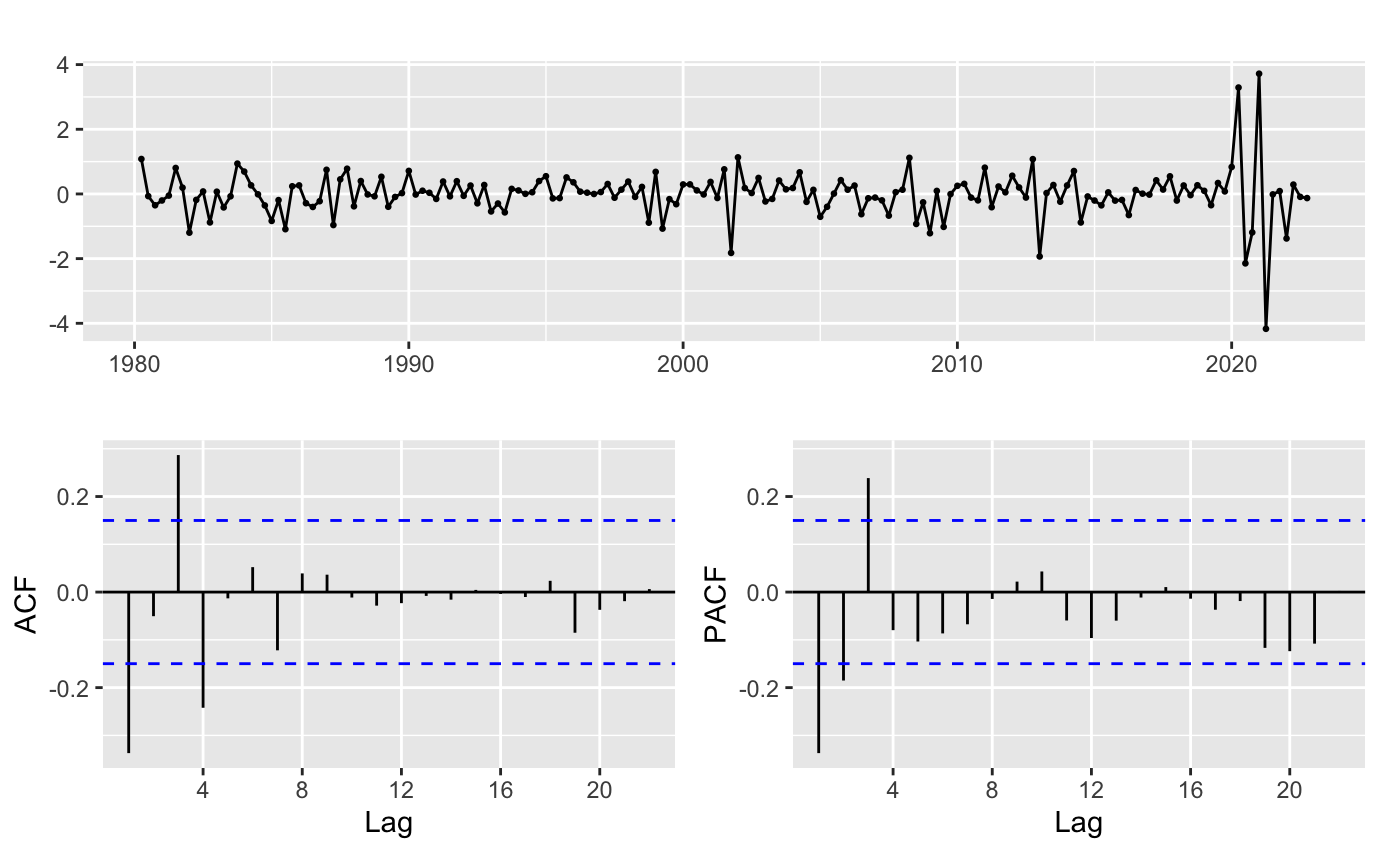
After seasonal difference and ordinary difference, the ACF and PACF plots are fairly stationary. lag of 1 and 3 is significant in both of the plots so p = 1,2,3 and q = 1,2,3
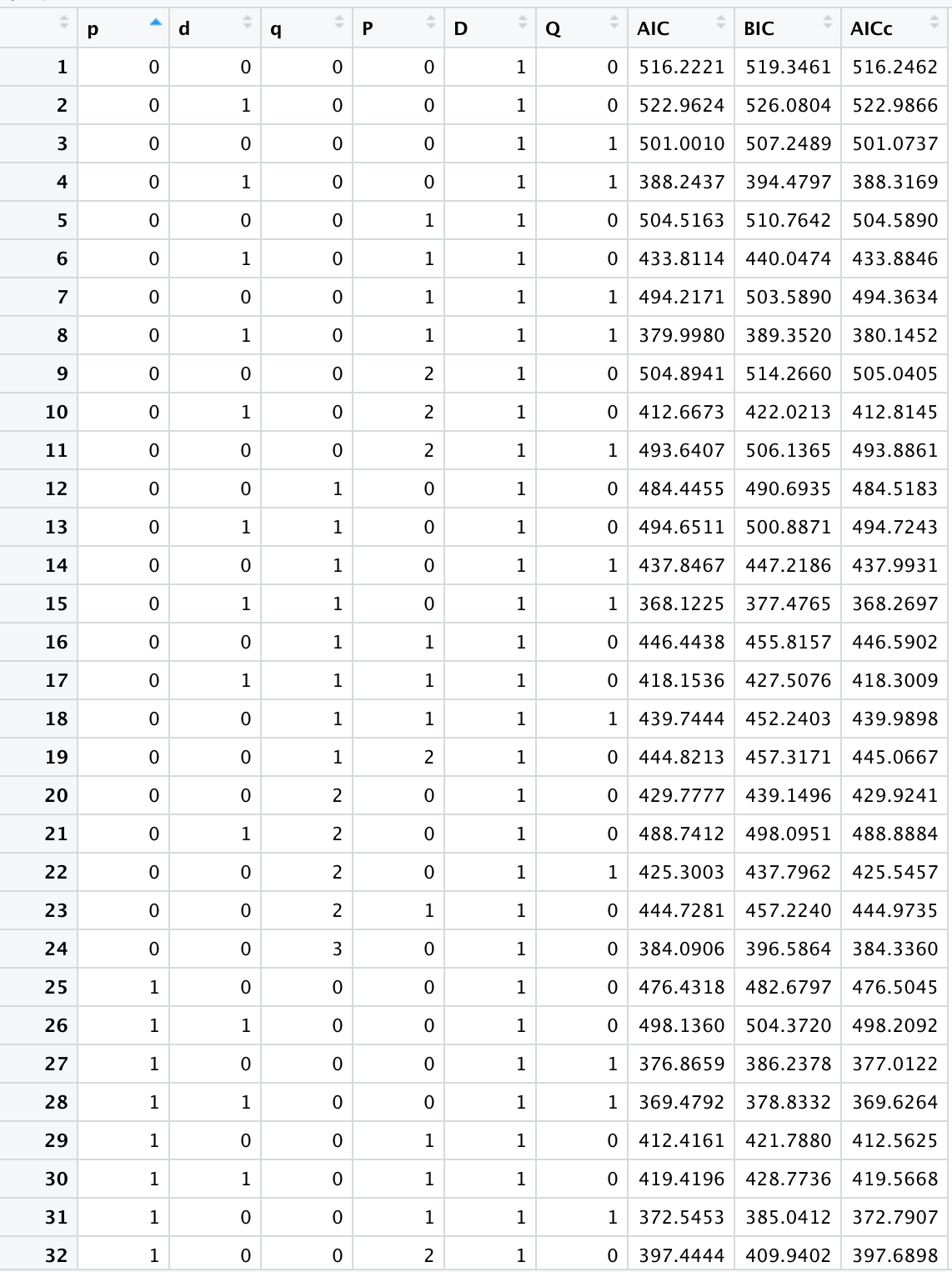
Figure 8. Min AIC, BIC, and ACIc Values



Based on the abouve the model with lowest AIC, BIC and ACIc values is model 35 (p = 1, d = 0, q = 1).According to the manual method result above, the ARIMA model p = 1, d = 0, q = 1 is the best.
Cross Validation
Figure 9. Cross Validation for ARIMAX Modle
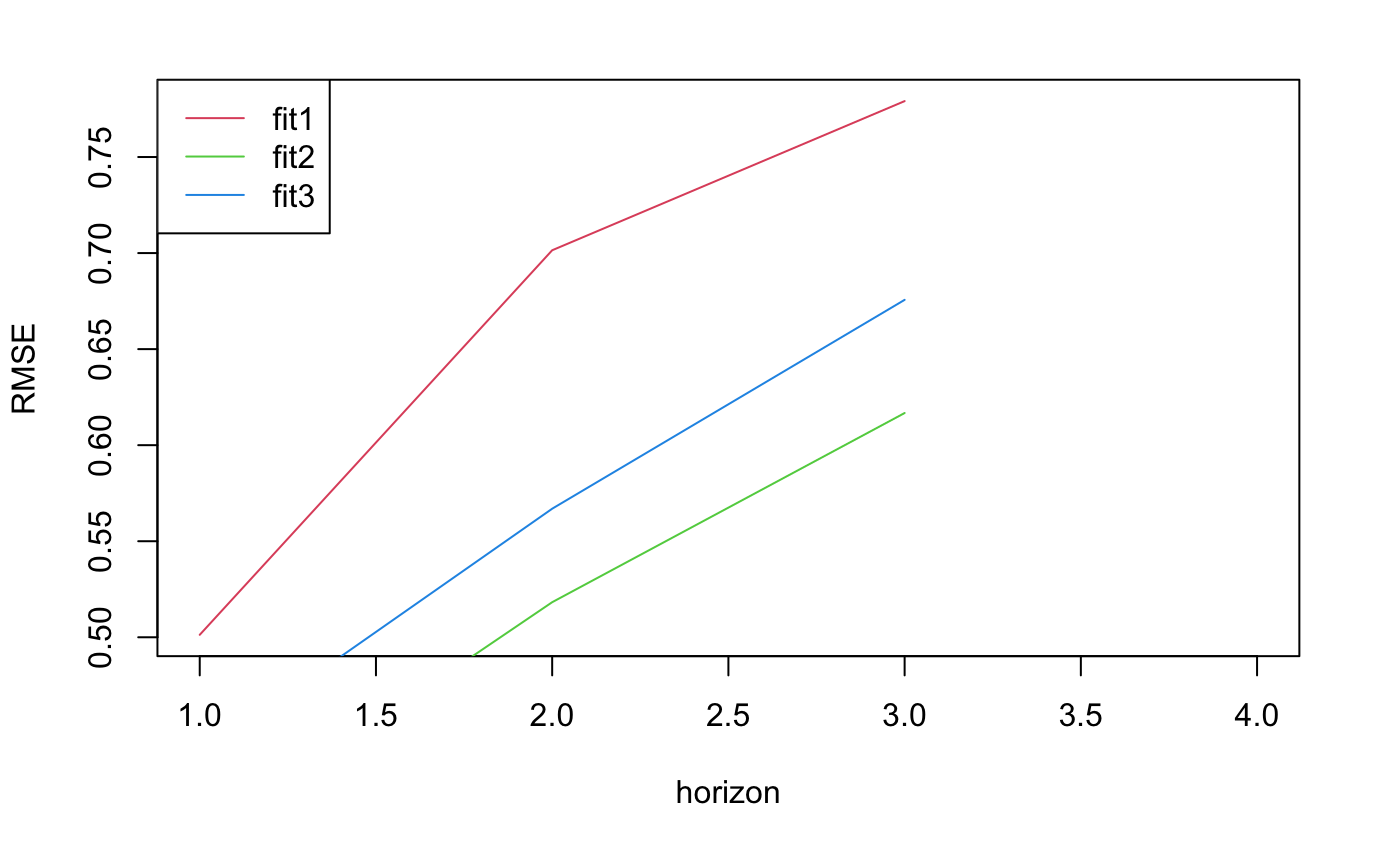
As seen in Figure 8 the result of cross-validation, the second model has lower RMSE except during the second period so the model ARIMAX(1,0,1) would be chosen.
Forecast
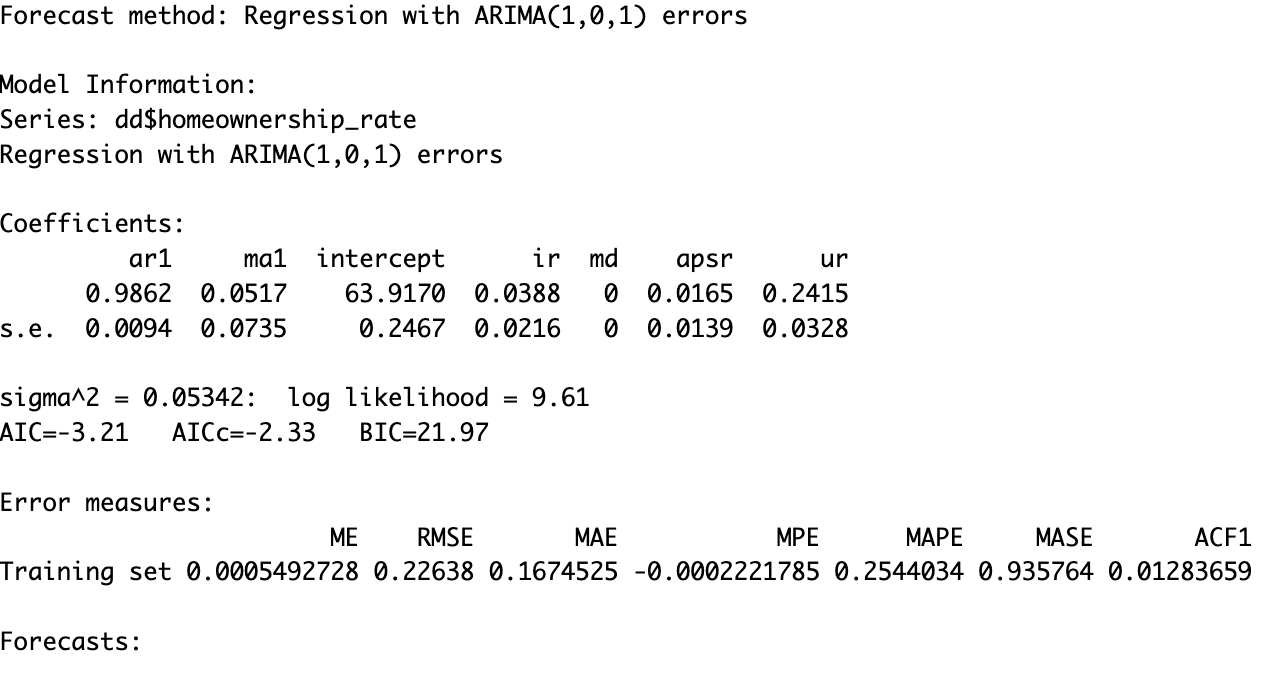
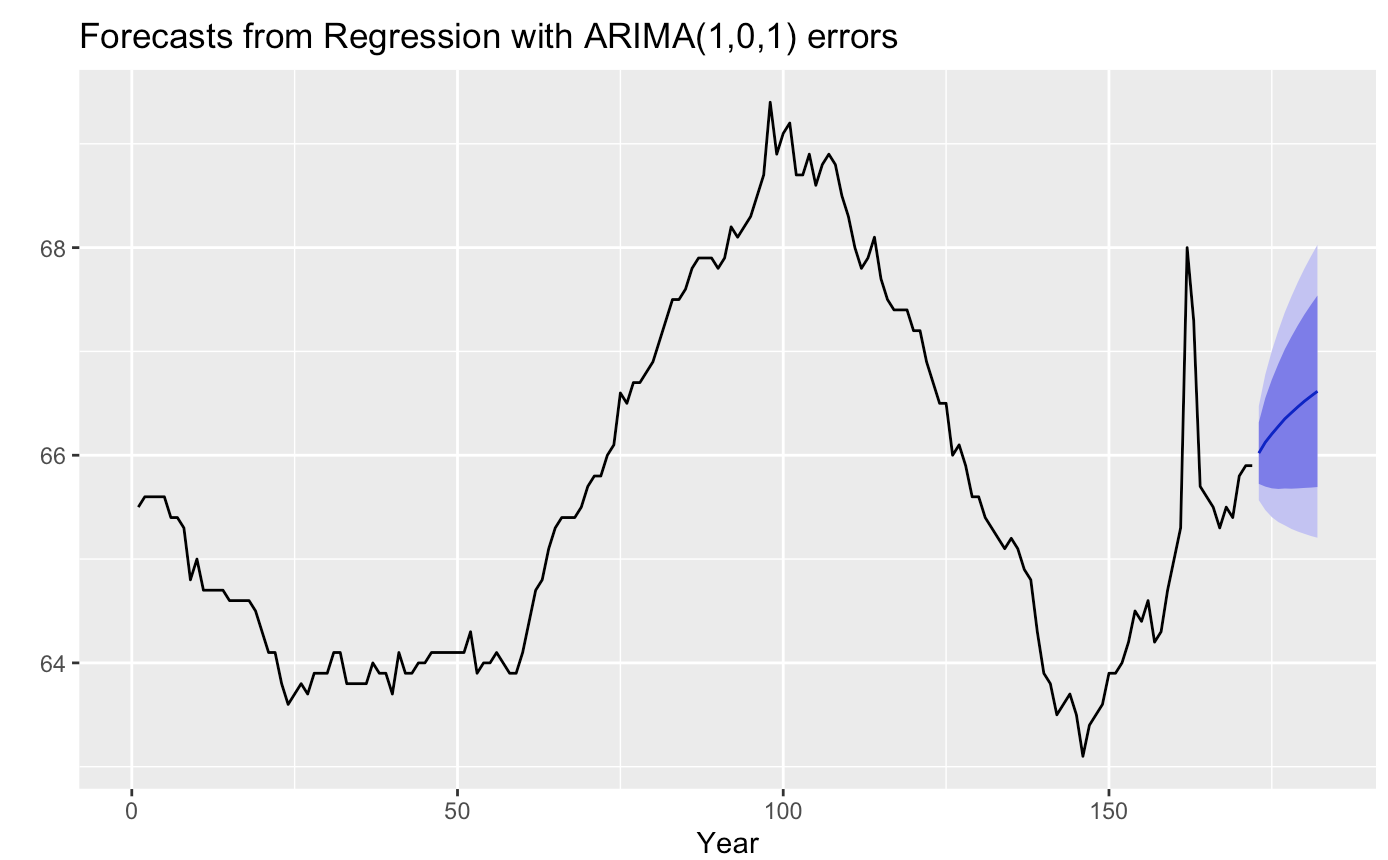
As per the prediction made by the ARIMAX(1,0,1) model, the level of the homeownership rate will remain the same in the near future, which means the increase in the interest rate and current uncertainty about the economy, may not affect the homeownership rate much.