Exploratory Data Analysis

Figure 1:

Figure 1 illustrates homeownership rates in the United States from 1980 to 2022. In the 1980s, the homeownership rate in the US declined due to economic challenges such as high-interest rates and inflation. The rate fell from 65.6% in 1980 to 63.8% in 1990. The homeownership rate in the US increased again during the 1990s due to a strong economy and low mortgage rates. The rate peaked at 67.3% in 2000. The homeownership rate in the US reached an all-time high of 69.2% in 2004. However, this increase was partly due to easy access to subprime mortgages, which led to the housing market crash in 2008. In the aftermath of the housing market crash, the homeownership rate in the US declined sharply, falling to 63.7% in 2016. This decline was due to tighter lending standards and a slow economic recovery. As of 2021, the homeownership rate in the US has rebounded slightly, reaching 65.8% in the fourth quarter of 2020..

Figure 2: Time Series Graph of Figure 1.

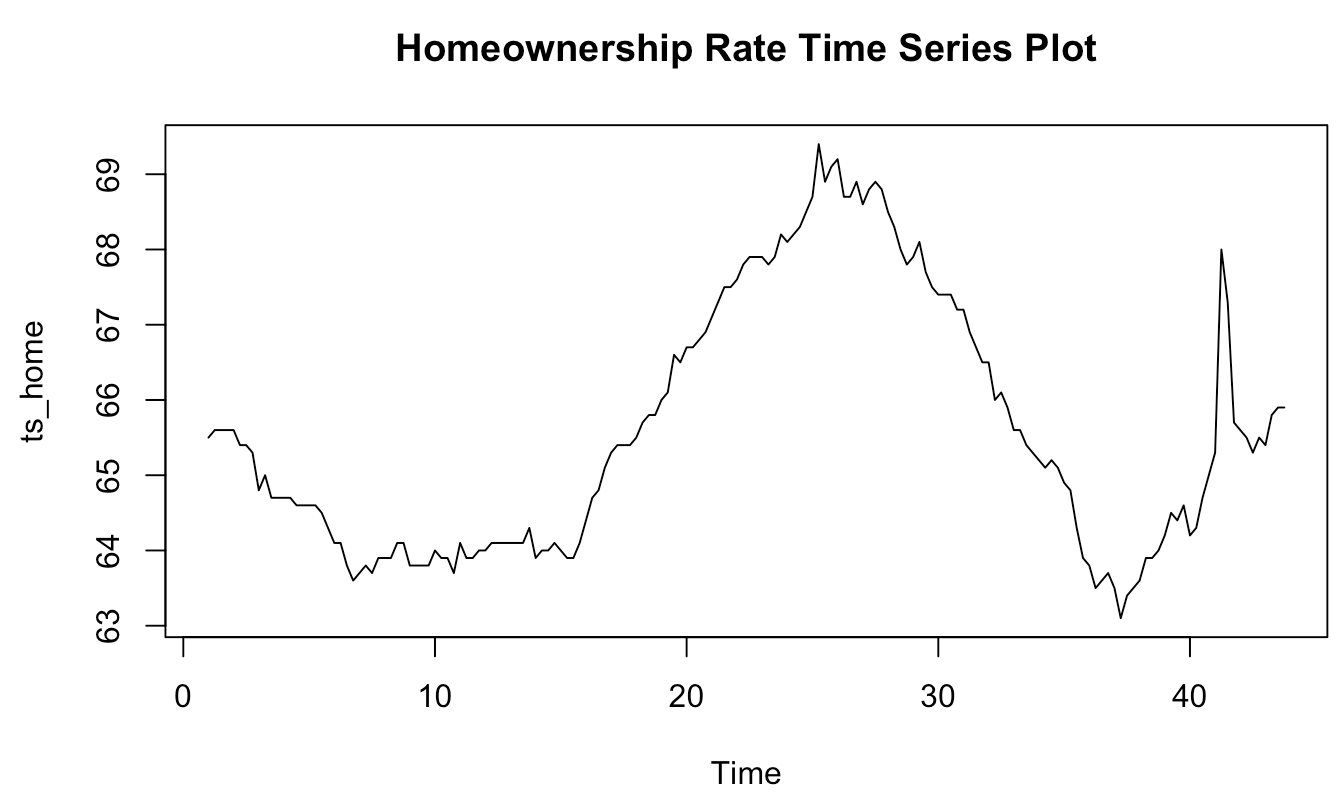
Similar to Figure 1, we see an upwards thrend in figure two with an expdentila increase starting in 2020 with mutiplicative tread.

Figure 3: Lag Plot

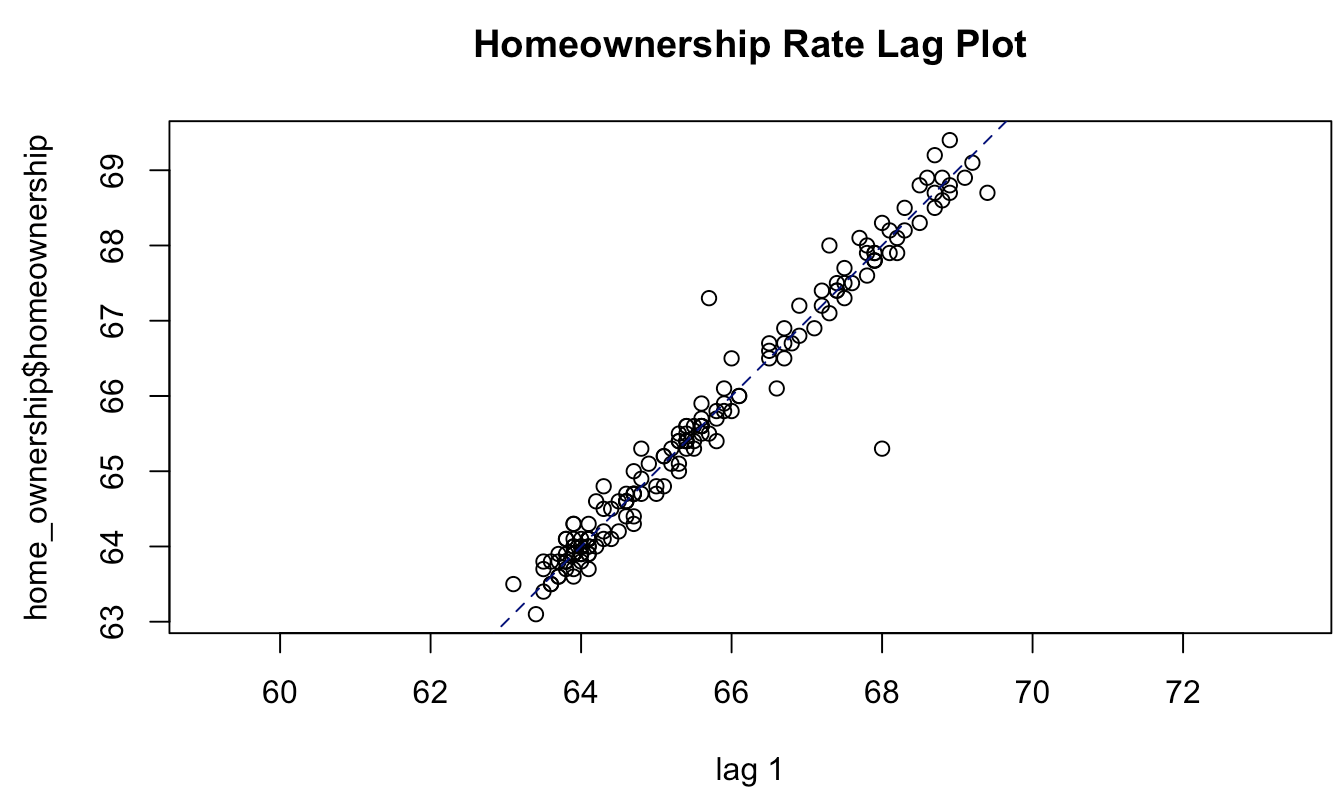
Figure 3, displays the simple moving average treand of figure 1.

Figure 4: Decomposition of Additive Time Series

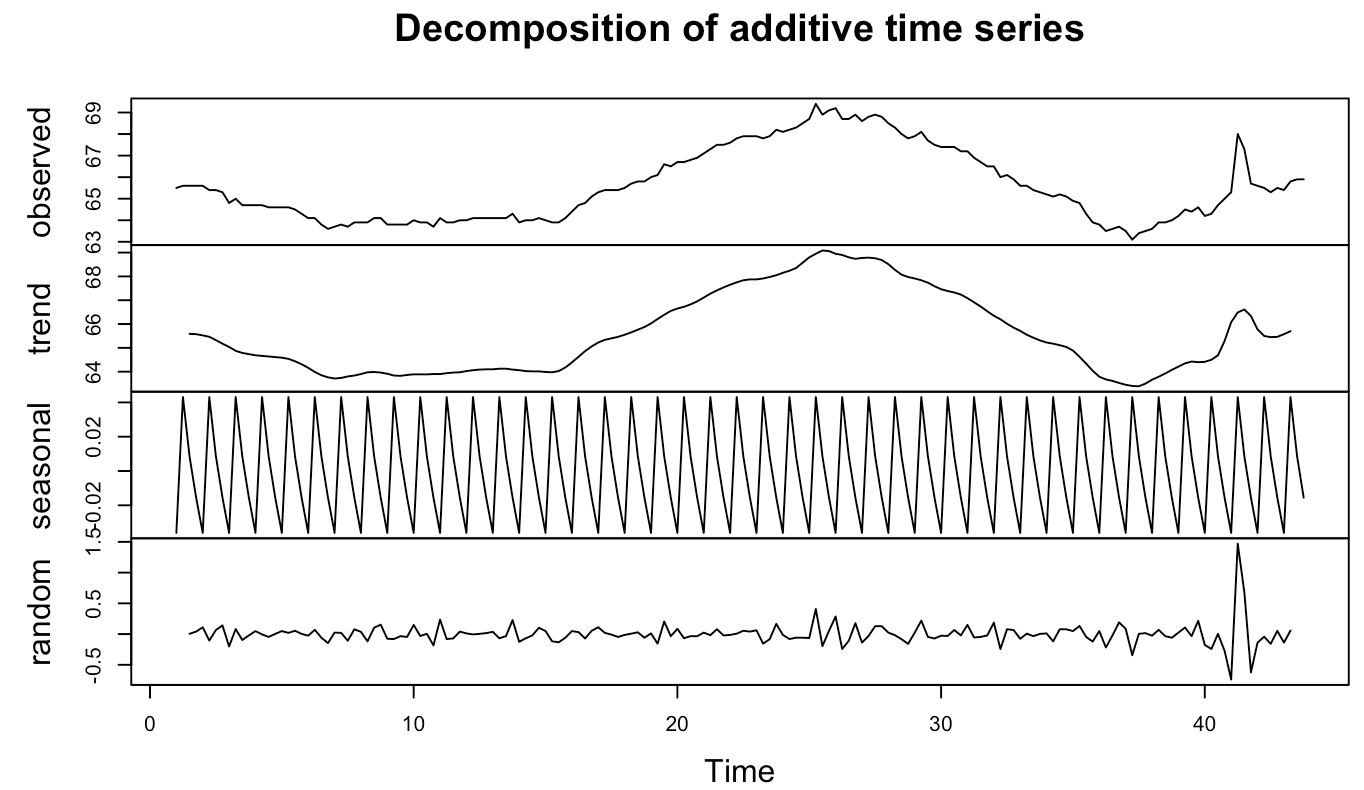
The decomposition plot above show that the trend is actually additive, multiplicative.

Figure 5a: Homeownership Rate ACF Plot

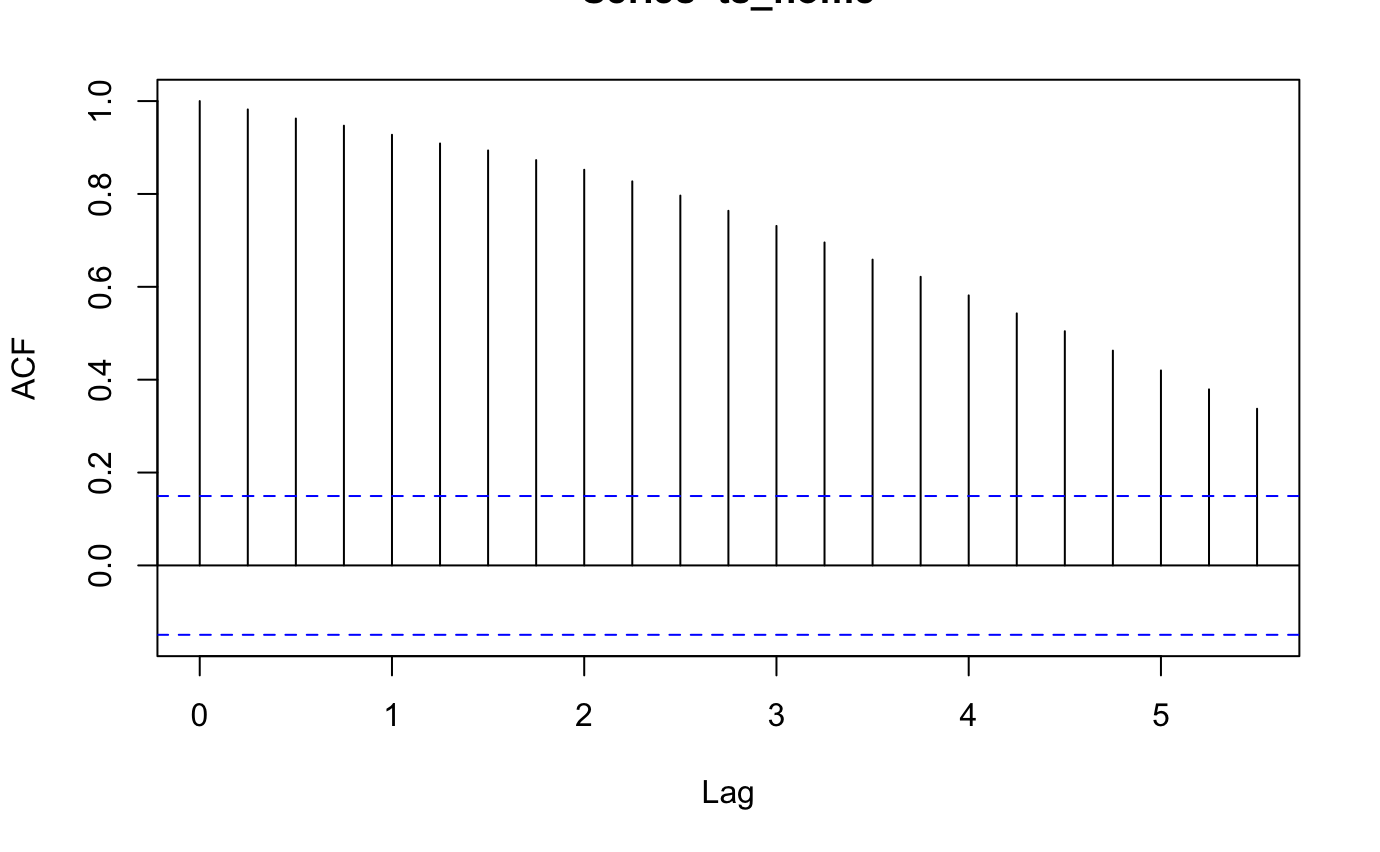
Based on figure 5, we can conclude that the data is not stationary, meaning it's statistical properties change over time. Simirarly the Augmented Dickey-Fuller Test (ADF Test) displayed on figure 6 shows that the data is not stationary. Therefore would need diffrenciating.

Figure 5b: Homeownership Rate Time Series PACF Plot

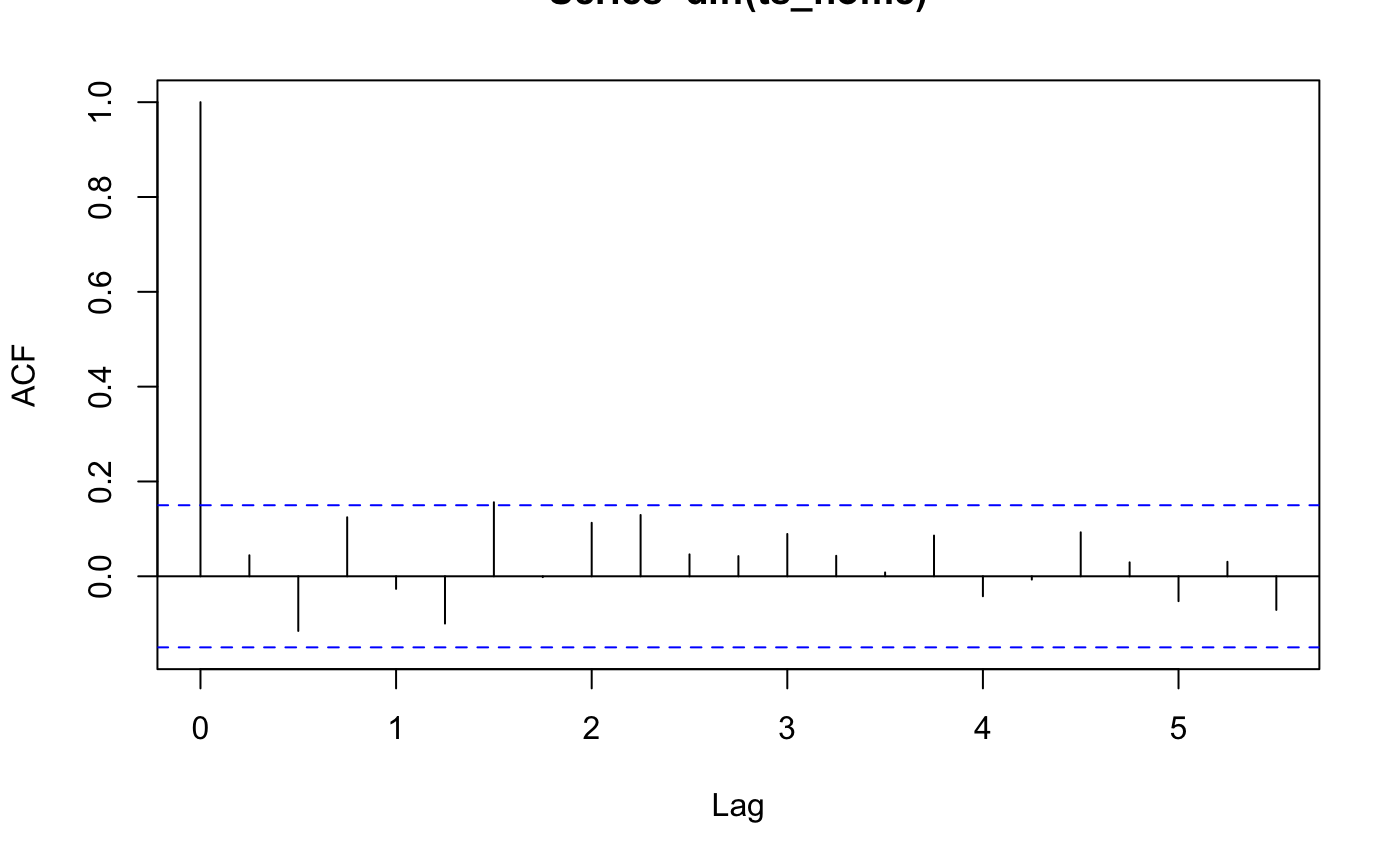
Figure 6: Augmented Dickey-Fuller Test

Figure 7: Homeownership Rate ACF Plot of Differianted Data

Based on Figure 5, we can conclude that the data is not stationary, meaning its statistical properties change over time. So we differentiated the data, and as shown in Figure 7, the ACF plot indicated that the differentiated plot is stationary. Similarly, the ADF Test of the differentiated data in Figure 8 shows that the diffracted data is stationary.

Figure 8: Augmented Dickey-Fuller Test of Differianted Data

Figure 9: Moving Average of Homeownership Rate Data.